Notes on Marimo
Marimo is a reactive notebook system in Python. Here are some thoughts on it:
- Reactivity is implemented by re-writing Python expressions in the cells by means of (it appears) static analysis. The on-disk format is the rewritten expression.
- The rewrite makes all inputs and outputs explicit parameters/return values. This rewrite turns global variables into function parameters/returns
- This work well for the (simple) cases tested so far. Not sure it is a that big advantage for an experienced Python developer but perhaps it is for newcomers.
- A reactive notebook system “Pluto” has been available for the Julia ecosystem for some time.
- There is a nice two-dimensional notebook layout in Marimo
- The on-disk format is extremely easy to read, and automatic watch functions means editing outside of Marimo works very well
- The usual IDE assists seem to work well in the notebook
- And in the time it has taken me to put together these notes and some experiments I seen they’ve been bought by Corewave: https://marimo.io/blog/joining-coreweave !
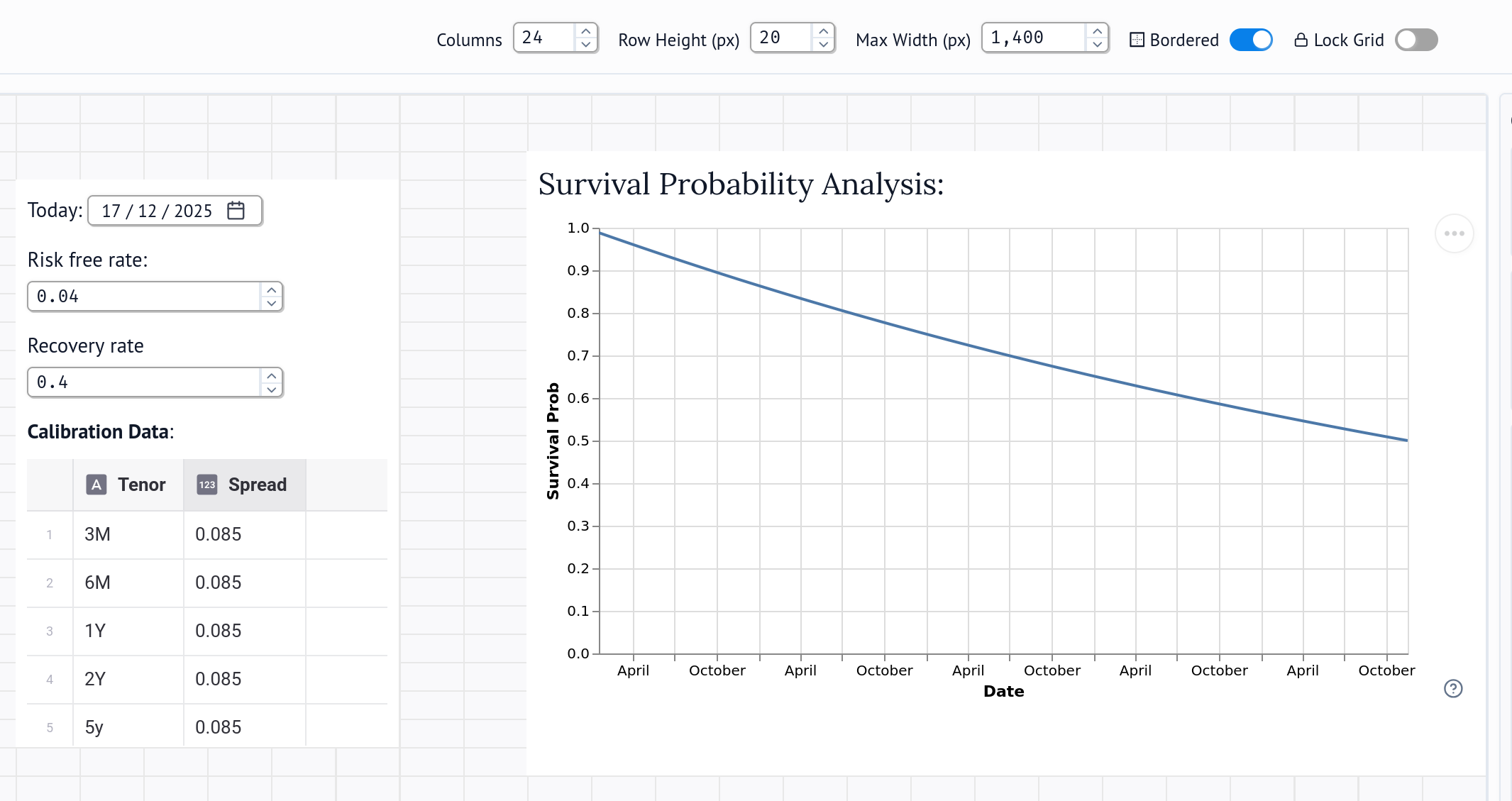
And here is a very quick illustration of the two-dimensional layout:
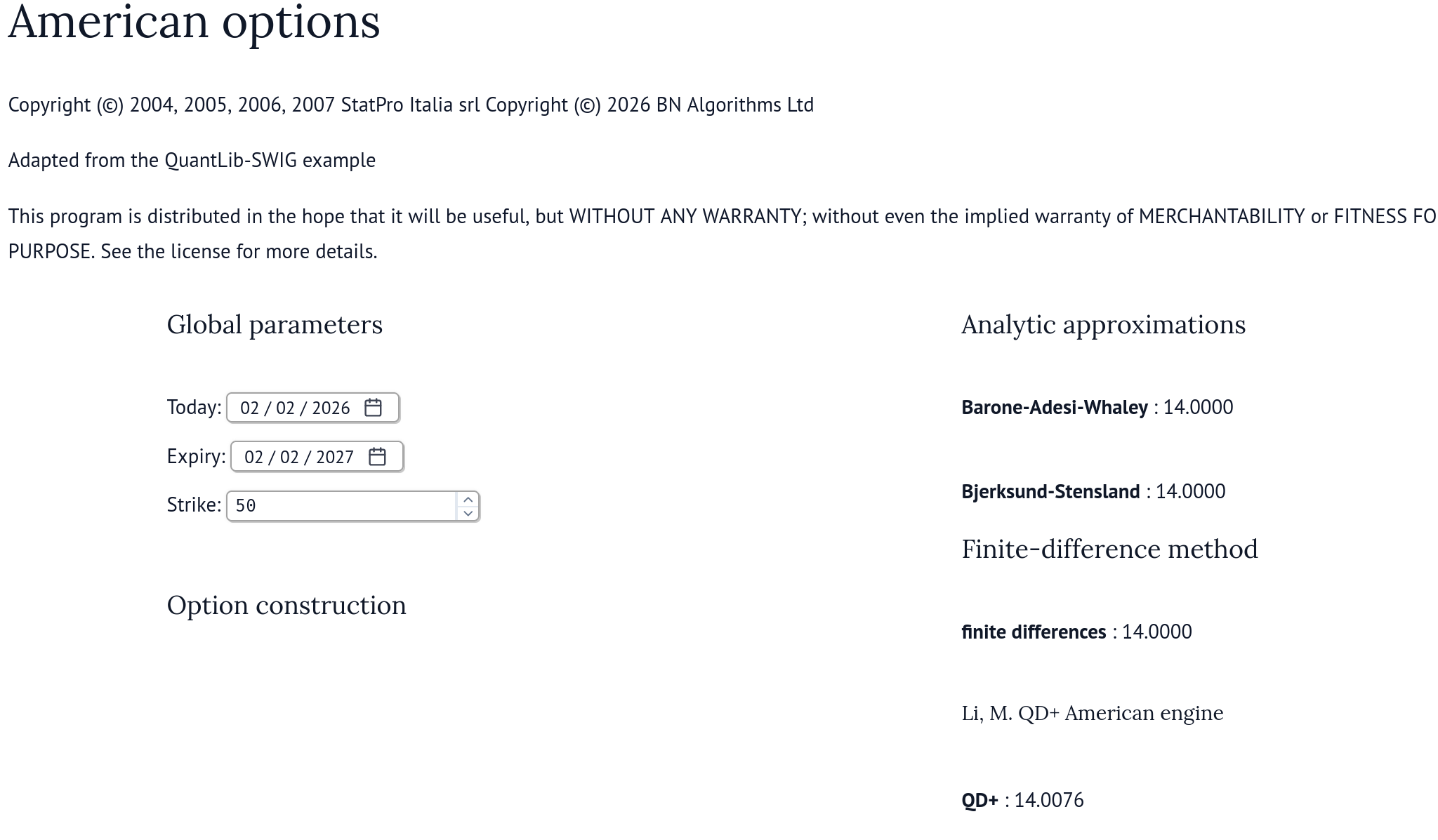
Here is a quick conversion of QuantLib American Option example:
American options
Copyright (©) 2004, 2005, 2006, 2007 StatPro Italia srl Copyright (©) 2026 BN Algorithms Ltd
Adapted from the QuantLib-SWIG example
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the license for more details.
import QuantLib as ql
import pandas as pd
import qlutils
Global parameters
todaysDate = mo.ui.date()
expiryDate = mo.ui.date()
K = mo.ui.number(1, 100, step=0.1)
mo.vstack([ mo.md(f"Today: {todaysDate}"),
mo.md(f"Expiry: {expiryDate}"),
mo.md(f"Strike: {K}"),
])
Option construction
ql.Settings.instance().evaluationDate = qlutils.qlDate(todaysDate.value)
exercise = ql.AmericanExercise(qlutils.qlDate(todaysDate.value),
qlutils.qlDate(expiryDate.value))
payoff = ql.PlainVanillaPayoff(ql.Option.Put, K.value)
option = ql.VanillaOption(payoff, exercise)
Market data
underlying = ql.SimpleQuote(36.0)
dividendYield = ql.FlatForward(qlutils.qlDate(todaysDate.value), 0.00, ql.Actual365Fixed())
volatility = ql.BlackConstantVol(qlutils.qlDate(todaysDate.value), ql.TARGET(), 0.20, ql.Actual365Fixed())
riskFreeRate = ql.FlatForward(qlutils.qlDate(todaysDate.value), 0.06, ql.Actual365Fixed())
process = ql.BlackScholesMertonProcess(
ql.QuoteHandle(underlying),
ql.YieldTermStructureHandle(dividendYield),
ql.YieldTermStructureHandle(riskFreeRate),
ql.BlackVolTermStructureHandle(volatility),
)
Pricing
We’ll collect tuples of method name, option value, and estimated error from the analytic formula.
Analytic approximations
option.setPricingEngine(ql.BaroneAdesiWhaleyApproximationEngine(process))
BaroneAdesiNPV = option.NPV()
mo.md(f'**Barone-Adesi-Whaley** : {BaroneAdesiNPV:.4f}')
option.setPricingEngine(ql.BjerksundStenslandApproximationEngine(process))
mo.md(f'**Bjerksund-Stensland** : {option.NPV():.4f}')
Finite-difference method
timeSteps = 801
gridPoints = 800
option.setPricingEngine(ql.FdBlackScholesVanillaEngine(process, timeSteps, gridPoints))
mo.md(f'**finite differences** : {option.NPV():.4f}')
Li, M. QD+ American engine
option.setPricingEngine(ql.QdPlusAmericanEngine(process))
mo.md(f'**QD+** : {option.NPV():.4f}')
Leif Andersen, Mark Lake and Dimitri Offengenden high performance American engine
option.setPricingEngine(
ql.QdFpAmericanEngine(process, ql.QdFpAmericanEngine.accurateScheme())
)
mo.md(f'**QD+ fixed point** : {option.NPV():.4f}')
Binomial method
timeSteps_1 = 801
r =[]
for tree in ['JR', 'CRR', 'EQP', 'Trigeorgis', 'Tian', 'LR', 'Joshi4']:
option.setPricingEngine(ql.BinomialVanillaEngine(process, tree, timeSteps_1))
r.append( mo.md(f'**Binomial ({tree}) differences** : {option.NPV():.4f}'))
mo.vstack(r)
import marimo as mo
Produces following app: