A common problem in engineering, finance and science is of the form: you have a known non-linear function with some number of parameters (and also perhaps of some observed data). How do you best find the optimum parameters which, say, minimise the function?

The function could correspond to a goodness-of-fit of a model to some observed data, or it could be a figure-of-merit of a parameterised design for say an optical system. Quite often finding this optimum is slow, but also programming the function to be optimised can be time consuming and error prone.

There is a vast amount of software available to do this, e.g.,

  • Excel’s inbuilt solver (this is probably the most widely used!)

  • Minimiser functions from Numerical Recipes

  • Fortran PDA routines

  • SciPy/R/other OSS and MatLab/Commercial routines

  • etc

This is all obvious software to try. Perhaps less obvious is using machine learning software to solve this (non-machine-learning!) problem.

In particular I’ve had a great deal of success recently in applying PyTorch ( home page ) to this non-linear optimisation problem. It is possible to use PyTorch without any knowledge or reference to neural networks or machine learning, i.e., use PyTorch simply as as a numpy substitute.

The initial results are described in this arXiv paper (subsequently also presented at ADASS in College Park) and since then there have two more applications which have benefited greatly from this approach.

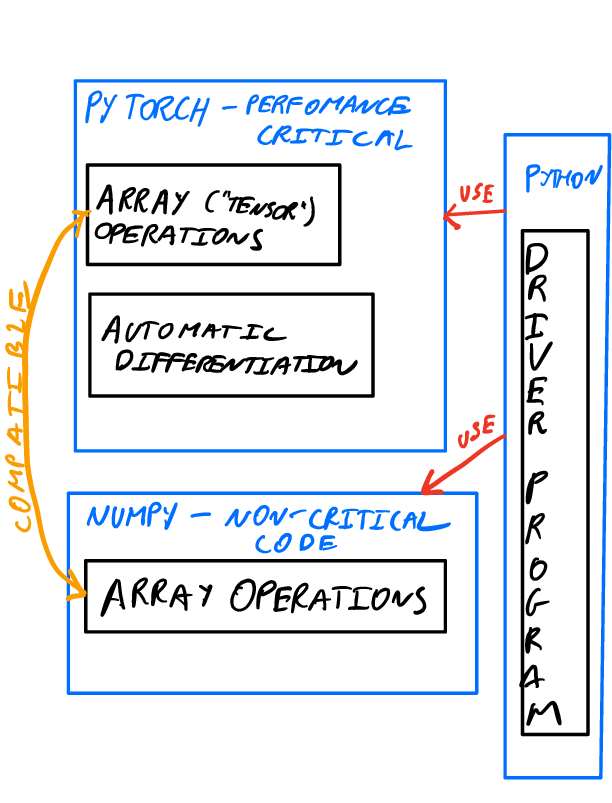
  1. Implement the problem to be optimised/function to be minimised in Numpy/Python. This is an environment that is fast to develop in and familiar to many people (e.g., if they are coming from Matlab as well as Python). Do the optimisation using standard scipy minimisers

  2. Identify the likely bottleneck parts of the code, using standard Python and OS profiling tools (I find sudo perf top to often be sufficient!)

  3. Re-implement the bottleneck parts in PyTorch. PyTorch is able to operate on NumPy datastructures so the new modules can seamlessly interact with the existing NumPy code

  4. Use PyTorch GPU offloading to accelerate individual function evaluations. Function valuation can then be fed into standard scipy optmisers without need for further modifications.

  5. Use PyTorch automatic differentiation to accelerate the calculation of derivatives. These calculated derivatives can also be passed into standard scipy optmisiers, avoiding the need for finite difference estimation and providing significant and easy acceleration with minimal for modifying code

high level overview

Summary

The summarise the benefits I’ve seen:

  • About a 10x improvement in time-to-solution from the automatic differentiation

  • An additional 10x improvement in time-to-solution from automatic GPU utilisation

Most importantly, both of these benefits came with extremely little programming effort. Engineers working with me with for example background in Matlab are easily able to write high-quality PyTorch programs that execute efficiently on GPUs within a month of beginning to learn it.

So, if you have a tough optmisation problem to solve, I recommend PyTorch as your first port of call – no knowledge of machine learning needed!